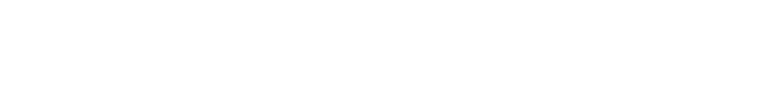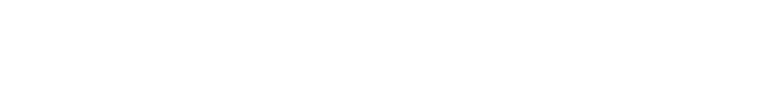Deine Rechnung ergibt jedenfalls ein anderes Resultat.
Ich kann dir höchstens erklären, was ich gemacht / überlegt habe.
Zuerst wollte ich nur wissen, wie ich es rechnen muss um zu erfahren, wieviele Versuche ich brauche, um eine bestimmte Wahrscheinlichkeit zu erreichen. Im I-Net habe ich dann folgende Formel gefunden:
n = Versuche
a = Zu erreichende Wahrscheinlichkeit
p = Wahrscheinlichkeit für einen positiven Fall
ln(1-a) / ln(1-p) = n
Meine Werte eingesetzt sieht's so aus:
ln(1-0.9) / ln(1-0.0005) = 4604.0188
Nun weiss man, dass man mit der Wahrscheinlichkeit von 0.05% für einen 90%igen Erfolgsfall 4605 Versuche braucht.
Danach wollte ich das ganze ein wenig ändern und die Gleichung so ändern, dass ich als Resultat die erreichte Wahrscheinlichkeit habe, wenn ich als Variabel die Anzahl Versuche in die Gleichung einsetze. Dazu musste ich aber vom ln(1-0.9) ja das 0.9 herausbringen. Um das zu können, musste ich wissen, wie ich das ln auflöse.
Die Lösung war, wie br@insc@n zuerst schon richtig gesagt hatte, das e^. Irgendwie hab ich danach aber die Gleichung falsch gemacht, weshalb mein Resultat immer falsch war. adipictures hat dann weitergeholfen. Die schlussendlich, für mich, richtige Formel ist:
n = Anzahl Versuche
x = Wahrscheinlichkeit für einen positiven Fall
1-e^(n*ln(1-0.0005)) = x